玖的数学&算法录
0%

2023牛客寒假算法训练营1

发表于 更新于
本文字数： 7.4k 阅读时长 ≈ 7 分钟

感受：感觉整场都是诈骗题和一小部分妙妙结论题。

难度：

签到：ALCH

简单：DKM

中等偏下：GFE

中等偏上：BIJ

A.World Final? World Cup! (I)

题意：

本题需要模拟一次点球大战，约定对战双方为AB，按照ABABABABAB的方式来进行罚点球，即交替点球，各罚五次，A先手，若进球则加一分。

问：从第几球开始胜负已经出来了，如果点完十球仍不知道结果，则输出 -1 。

题解：模拟

约定 cntA 为 A 的进球得分， cntB 为 B 的进球得分，nowA 为 A 剩下几次罚球，nowB 为 B 剩下几次罚球。

模拟每一场的进球情况，并且保证每一次进球后对 A 均有

$$\displaystyle cntA + nowA < cntB 且 cntB + nowB < cntA$$

同样对 B 也有

$$\displaystyle cntB + nowB < cntA 且 cntA + nowA < cntB$$

代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void JiuCherish(){
    std::string s;
    std::cin >> s;
    s = " " + s;
    int n = s.length();
    int cntA = 0,cntB = 0;
    int nowA = 5,nowB = 5;
    for(int i=1;i<n;i++) {
        if(i & 1) {
            if(s[i] == '1') ++cntA;
            nowA--;
            if(cntA + nowA < cntB) {
                std::cout << i << endl;
                return;
            } else if(cntB + nowB < cntA) {
                std::cout << i << endl;
                return;
            }
        } else {
            if(s[i] == '1') ++cntB;
            nowB--;
            if(cntB + nowB < cntA) {
                std::cout << i << endl;
                return;
            } else if(cntA + nowA < cntB) {
                std::cout << i << endl;
                return;
            }
        }
    }
    std::cout << -1 << endl;
}

官方题解：

检查前 i 场是否能确定结果的方式：剩下的 10-i 场里，假设最后 A 最高 A1 分、最低 A2 分，B 最高 B1 分，最低 B2 分，其确定胜负当前仅当：

$$\displaystyle (A1 - B2) * (B1 - A2) < 0$$

上面式子分成两部分：第一部分为：A最好时能赢B吗，第二部分为：B最好时能赢A吗。

官方题解思路的代码（自写的）：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void JiuCherish(){
    std::string s;
    std::cin >> s;
    int n = s.length();
    int A1 = 0,A2 = 5;
    int B1 = 0,B2 = 5;
    for(int i=0;i<10;i++) {
        if((i + 1) & 1) {
            if(s[i] == '1'){
                ++A1;
                ++A2;
            }
            A2--;
        }
        else {
            if(s[i] == '1'){
                ++B1;
                ++B2;
            }
            B2--;
        }
        if((A1 - B2) * (B1 - A2) < 0) {
            std::cout << i + 1 << endl;
            return;
        }
    }
    std::cout << -1 << endl;
}

B.World Final? World Cup! (II)

题意：

本题需要你模仿一支队伍进行联赛征程。

规则：踢若干场比赛。每赢一场（进球数大于对方）比赛得3分，每输一场比赛（进球数小于对方）得0分，每次平局（进球数等于对方）得1分。

已知接下来的 n 轮比赛中，某队一共进行了 x 个球，而某队的 n 个对手和某队的比赛一共进了 y 个球，求 这 n 轮中有多少种不同的比赛结果使得本赛季某队获得至少 m 分。

对于两种比赛结果：若 n 轮比赛中至少有一场的比分不一样，就认为两种比赛结果不同。

数据范围

$$1 \leq n \leq 40,0 \leq m \leq 120, 0\leq x,y\leq 100$$

输出结果，并让答案对 998244353取模。

题解：

C.现在是，学术时间 (I)

题意：

一位教授可以发表多篇论文，每篇论文有一个引用量。定义一位教授的H指数为使得 “ 该教授发表的所有论文中，有至少 H 篇论文的引用量大于等于 H “这一命题成立的最大的 H。

现在某院决定以最优的方式重新分配这些论文，他可以任意指定一篇论文由谁发表，也可以规定每篇论文只能被一位教授，一位教授可以发表多篇论文。

在重新分配后的第 i 位教授的 H 指数为 h_i , 院长希望最大化所有教授的 H 指数之和，请帮忙计算这一最大的值是多少？

数据范围：

有 T 组数，n 个教授数量， a_i 表示论文发表后的引用量。

$$\displaystyle 1\leq T \leq 10^5 , 1\leq n\leq 10^5, 0\leq a_i \leq 10^9$$

且保证

$$\displaystyle \sum n\leq 5 \times 10^5$$

题解：模拟

根据 H 指数的定义，有 H 篇论文的引用量大于等于 H , 那么不妨每个人都分配一篇，容易发现：除开 a[i] == 0 的情况，其他分配方式都是成立的。

代码：
1
2
3
4
5
6
7
8
9
10
11
12
void JiuCherish(){
   int n;
   std::cin >> n;
   for(int i=1;i<=n;i++) std::cin >> a[i];
   int ans = 0;
   for(int i=1;i<=n;i++) {
      if(a[i] >= 1) {
         ++ans;
      }
   }
   std::cout << ans << endl;
}

D.现在是，学术时间 (II)

题意：

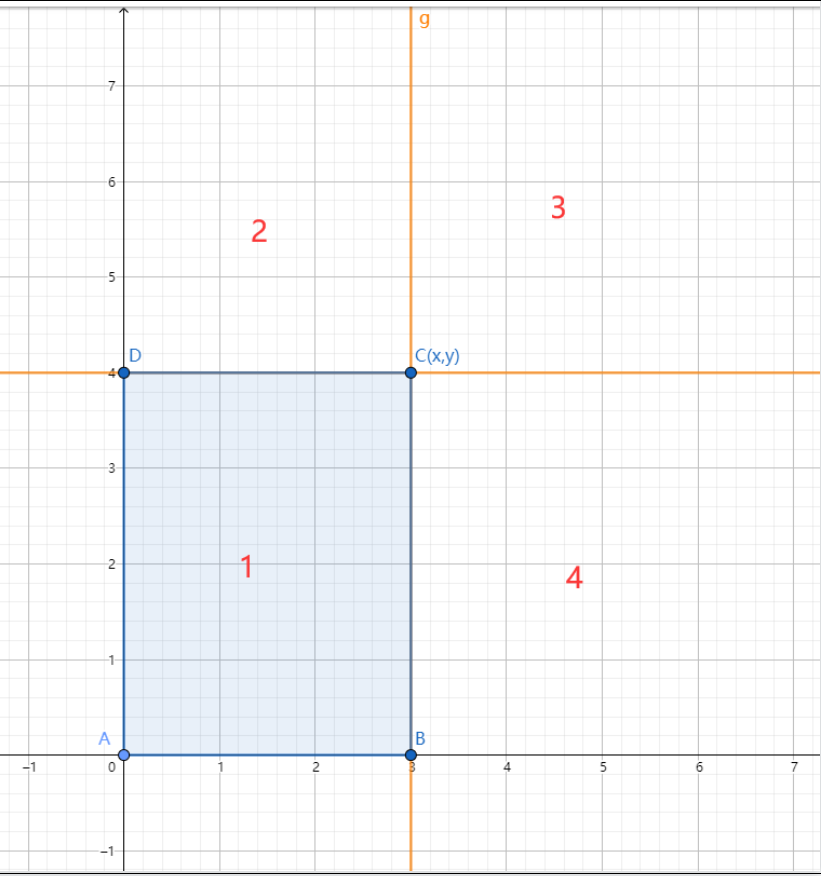
给出一个由平面上两点(0,0),(x,y)所确定的GT目标框和一个点P(xp,yp)。请你求出在所有以P点作为其中一个顶点且边都平行于坐标轴的预测目标框中，可以使其与GT目标框取到的最大IOU为多少。

定义两个矩形A,B的IOU为两个矩形交集部分的面积除以两个矩形并集部分的面积。

数据范围：

T：测试用例

$$1 \leq T \leq 10^4 , 0 < x,y,x_p,y_p \leq 1000$$

对误差不超过1e-4 即是正确，

（大概懂了，不想写）

官方题解：贪心、数学、分类讨论

image

  • 另一个矩形顶点一定是ABCD之一；
  • 考虑P点坐标的四种情况，即右图四个区域
  • 区域1：枚举A、B、C、D作为另一顶点的四种情况，取最大IOU；（易证）
  • 区域3：取A作为另一顶点； （不易证）
  • 区域2：枚举A、B作为另一顶点的两种情况，选较大的IOU； （易证）
  • 区域4：枚举A、D作为另一顶点的两种情况，选较大的IOU； （易证）

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void JiuCherish(){
    double x,y,xp,yp;
    std::cin >> x >> y >> xp >> yp;
    double ans = 0;
    if(xp <= x && yp <= y) {
        ans = std::max(ans,1.0 * xp * yp / x / y);
        ans = std::max(ans,1.0 * (x - xp) * yp / x / y);
        ans = std::max(ans,1.0 * xp * (y - yp) / x / y);
        ans = std::max(ans,1.0 * (x - xp) * (y - yp) / x / y);
    } else if(xp <= x) {
        ans = std::max(ans, 1.0 * xp * y / (x * y + xp * (yp - y)));
        ans = std::max(ans, 1.0 * (x - xp) * y / (x * y + (x - xp) * (yp - y)));        
    } else if(yp <= y) {
        ans = std::max(ans, 1.0 * yp * x / (x * y + yp * (xp - x)));
        ans = std::max(ans, 1.0 * (y - yp) * x / (x * y + (y - yp) * (xp - x)));       
    } else {
        ans = std::max(ans,1.0 * x * y / xp / yp);
    }
    std::cout << std::fixed << std::setprecision(10) << ans << endl;
}

E.鸡算几何

F.鸡玩炸蛋人

G.鸡格线

题意：

有一个长度为 n 的数组 a ，你需要支持以下两种操作：

1、读入l，r，k 对区间**[l,r]** 中所有数字执行 a_i = f(a_i) 操作 k 次，其中

$$f(x) = round(10\sqrt{x}) , round为四舍五入函数$$

2、输出当前数组所有数字的和。

数据范围：

$$1 \leq n,m \leq 10^5, 0 \leq a_i \leq10^9, op\in(1 or 2)$$

$$1 \leq l \leq r \leq n ,1\leq k \leq10^5$$

题解：数据结构、模拟

f(x)经过不多次数的操作会收敛到一个不变的值，即：不动点。

该不动点有三个：0、99、100。

因此总的操作次数不会太大。

考虑用set来存所有未到达的x_0 的下标。

对该数字进行修改。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int f(int x) {
    return round(10 * sqrt(x));
}
void JiuCherish(){
    int n,m;
    std::cin >> n >> m;
    std::set<int> s;
    i64 sum = 0;
    for(int i=1;i<=n;i++) {
        std::cin >> a[i];
        sum += a[i];
        if(f(a[i]) != a[i]) s.insert(i);
    }
    s.insert(n + 1);
    while(m --) {
        int op;
        std::cin >> op;
        if(op == 1){
            int l,r,k;
            std::cin >> l >> r >> k;
            int pos = l;
            while(1) {
                int nxt = (*s.lower_bound(pos));
                if(nxt > r) break;
                for(int i=1;i<=std::min(k,15);i++) {
                    sum -= a[nxt];
                    a[nxt] = f(a[nxt]);
                    sum += a[nxt]; 
                }
                if(f(a[nxt]) == a[nxt]) {
                    s.erase(nxt);
                }
                pos = nxt + 1;
            }
        } else {
            std::cout << sum << endl;
        }
    }
}

H.本题主要考察了DFS

题意：

有一款拼图游戏，其拼图是由 n*n 个大小为 1*1 的拼图块组成，每个拼图块都是正方形的 1*1 拼图块基础上生成，生成方法：对于每一条边，可以选择不变（记为 0 ）、向里削出一个半圆形的缺口(记为 1 )、向外补上一个半圆形的凸出(记为 2 )三种操作之一，一个拼图块是由一个长度为 4 的字符串描述，分别表示着上右下左四条边的顺序。

其中，每块拼图还有一个制作成品 p ，对于一块削去了 x 个半圆、补上了 y 个半圆的 1 * 1 拼图，其制做成本为 p = 10 - x + y

现会隐藏其中一块，并打乱 n * n - 1 块拼图，告诉你对应的字符串，现在需要你完成该游戏，还原拼图原本的样子，输出还原后缺失拼图块的制作成本。

题解：模拟

因为对于结果来说无论如何都是能拼成的，因此只需要考虑有几个削去的半圆和补上的半圆即可。

代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void JiuCherish(){
    int n;
    std::cin >> n;
    int sum = 0;
    for(int i=1;i<=n * n - 1;i++) {
        sum += 10;
        for(int j=1;j<=4;j++) {
            std::cin >> c[i][j];
            if(c[i][j] == '1') sum--;
            else if(c[i][j] == '2') sum++;
        }
    }
    int total = n * n * 10;
    std::cout << total - sum << endl;
}

I.本题也主要考察了DFS

J.本题竟也主要考察了DFS

K.本题主要考察了dp

题意：

给你一个长度为 n 的字符串， 要求之中恰好有 m 个字符是 1 。

现在，规定对于原序列中一个长恰好为 3 的子区间（子区间是连续的），若之中 1 的个数多于 0 的个数，那么称为 坏区间。

请求出满足条件的字符串中，坏区间总数最少的字符串有几个坏区间。

数据范围：

$$\displaystyle 1\leq m \leq n \leq 1000$$

题解一：模拟、贪心、暴力

以100100100….的形式去构造字符串，保证前面基本上没有坏区间，最后0用完之后将多余的1补上，由于数据范围较小，所以直接暴力去遍历构造的字符串，统计坏区间即可。

代码一：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
void JiuCherish(){
   int n,m;
   std::cin >> n >> m;
   std::string s;
   std::cin >> s;
   int zero = n - m;
   int cnt = 0;
    //构造字符串
   for(int i=1;i<=n;i++) {
      if(i == 1) {
         s += '1';
         m--;
         continue;
      }
      if(zero && cnt != 2) {
         s += '0';
         cnt++;
         zero--;
         continue;
      }
      if(cnt == 2) {
         s += '1';
         cnt = 0;
         continue;
      }
      if(!zero) {
         s += '1';
      }
   }
   //暴力跑每一个字符串的位置，以及该位置的下一位和下下位。
   int ans = 0;
   for(int i=0;i<=n-3;i++) {
      int cnt0 = 0,cnt1 = 0;
      for(int j=i;j<=i+2;j++) {
         if(s[j] == '1') ++cnt1;
         else ++cnt0;
      }
      if(cnt1 > cnt0) ++ans;
   }
   std::cout << ans << endl;
}

L.本题主要考察了运气

题意：

某p–j–s–k游戏中有20名原创角色，分别属于5个团体，每个团体恰好4个人，为了猜出某个人最爱的角色，他会回答以下两类问题：

1、ta属于第 i (from 1 to 5) 个团体吗？

2、ta是第 i (from 1 to 5) 个团体的第 j (from 1 to 4) 个人吗？

在你百分百肯定之前，你需要不停的提问。

现在，你想知道，在选择最优的提问策略使提问数尽可能少的情况下，你的期望提问次数是多少次？本题要求输出该期望次数。

给定你式子

$$最终期望结果 = 3.45 + 0.05 * i$$

请输出 i 是多少（本题只有一个样例，且答案只会在 1~100）

题解：数学、概率

1、首先进行猜团：前三次猜到的概率均为 0.2 , 第四次猜的时候为 0.4 （如果猜不到那就是另一个，反之亦然）。

2、其次再去猜人：前两次猜到的概率为 0.25 , 第三次猜的时候为 0.5 理由同上。

故结果为

$$E(X) = 1 * 0.2 + 2 * 0.2 + 3 * 0.2 + 4 * 0.4 + 1 * 0.25 + 2 * 0.25 + 3 * 0.5 = 5.05$$

解得 i = 32

M.本题主要考察了找规律

题意：

X有 m 个章鱼仙贝，需要把这些仙贝分给 n 个朋友。

约定一开始X对所有朋友的好感度均为0，当X当前还剩下x（正数）个仙贝，并且送给了一位朋友y个仙贝，那么这位朋友对X的好感度增加y/x。

现在请帮X算一下，在最优送仙贝策略下，X和所有人的好感度之和最大为多少？

数据范围：

$$1 \leq n,m \leq 500$$

题解：dp

dp[i] [j] 表示已经给 i 个人分了仙贝，分出去了共 j 个收获的最大好感度是多少，即

$$\displaystyle dp[i][j] = \max_{k \leq j} (dp[i][j],dp[i - 1][j - k] + \frac{k}{m - (j - k)})$$

也就是枚举第 i 个人分到的仙贝数 k 。

因此答案是 dp[n] [m]

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
void JiuCherish(){
    int n,m;
    std::cin >> n >> m;
    dp[0][0] = 0;
    for(int i=1;i<=n;i++) {
        for(int j=0;j<=m;j++) {
            for(int k=0;k<=j;k++) {
                dp[i][j] = std::max(dp[i][j],dp[i - 1][j - k] + double(k) / (m - (j - k)));
            }
        }
    }
    std::cout << std::fixed << std::setprecision(9) << dp[n][m] << endl;
}