第 73 场双周赛
链接↓
第 73 场双周赛
2190.数组中紧跟 key 之后出现最频繁的数字
给你一个下标从 0 开始的整数数组 nums ,同时给你一个整数 key ,它在 nums 出现过。
统计 在 nums 数组中紧跟着 key 后面出现的不同整数 target 的出现次数。换言之,target 的出现次数为满足以下条件的 i 的数目:
0 <= i <= n - 2nums[i] == key 且nums[i + 1] == target 。
请你返回出现 最多 次数的 target 。测试数据保证出现次数最多的 target 是唯一的。
示例 1:
1
2
3
4
| 输入:nums = [1,100,200,1,100], key = 1
输出:100
解释:对于 target = 100 ,在下标 1 和 4 处出现过 2 次,且都紧跟着 key 。
没有其他整数在 key 后面紧跟着出现,所以我们返回 100 。
|
示例 2:
1
2
3
4
5
| 输入:nums = [2,2,2,2,3], key = 2
输出:2
解释:对于 target = 2 ,在下标 1 ,2 和 3 处出现过 3 次,且都紧跟着 key 。
对于 target = 3 ,在下标 4 出出现过 1 次,且紧跟着 key 。
target = 2 是紧跟着 key 之后出现次数最多的数字,所以我们返回 2 。
|
提示:
2 <= nums.length <= 10001 <= nums[i] <= 1000- 测试数据保证答案是唯一的。
分析:
根据题意,如果数组前一个数等于key,那么统计当前的值出现的次数,最后遍历1到1000,如果当前值出现的次数比答案大,那么将该值赋值到答案,最后返回即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| const int MAXH=1e5;
int a[MAXH];
class Solution {
public:
int mostFrequent(vector<int>& nums, int key) {
memset(a,0,size(a));
int n=nums.size();
for(int i=1;i<nums.size();i++){
if(nums[i-1]==key) a[nums[i]]++;
}
int ans=0;
for(int i=1;i<=1000;i++){
if(a[i]>a[ans]) ans=i;
}
return ans;
}
};
|
2191.将杂乱无章的数字排序
给你一个下标从 0 开始的整数数组 mapping ,它表示一个十进制数的映射规则,mapping[i] = j 表示这个规则下将数位 i 映射为数位 j 。
一个整数 映射后的值 为将原数字每一个数位 i (0 <= i <= 9)映射为 mapping[i] 。
另外给你一个整数数组 nums ,请你将数组 nums 中每个数按照它们映射后对应数字非递减顺序排序后返回。
注意:
- 如果两个数字映射后对应的数字大小相同,则将它们按照输入中的 相对顺序 排序。
nums 中的元素只有在排序的时候需要按照映射后的值进行比较,返回的值应该是输入的元素本身。
示例 1:
1
2
3
4
5
6
7
8
9
10
11
| 输入:mapping = [8,9,4,0,2,1,3,5,7,6], nums = [991,338,38]
输出:[338,38,991]
解释:
将数字 991 按照如下规则映射:
1. mapping[9] = 6 ,所有数位 9 都会变成 6 。
2. mapping[1] = 9 ,所有数位 1 都会变成 8 。
所以,991 映射的值为 669 。
338 映射为 007 ,去掉前导 0 后得到 7 。
38 映射为 07 ,去掉前导 0 后得到 7 。
由于 338 和 38 映射后的值相同,所以它们的前后顺序保留原数组中的相对位置关系,338 在 38 的前面。
所以,排序后的数组为 [338,38,991] 。
|
示例 2:
1
2
3
| 输入:mapping = [0,1,2,3,4,5,6,7,8,9], nums = [789,456,123]
输出:[123,456,789]
解释:789 映射为 789 ,456 映射为 456 ,123 映射为 123 。所以排序后数组为 [123,456,789] 。
|
提示:
mapping.length == 100 <= mapping[i] <= 9mapping[i] 的值 互不相同 。1 <= nums.length <= 3 * 1040 <= nums[i] < 109
分析:
题目意思是
| map值 |
8 |
9 |
4 |
0 |
2 |
1 |
3 |
5 |
7 |
6 |
| 原始值 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
即[991]所对应的值就是[669],以此类推
通过λ表达式去重写这个sort函数,将每个位上的数字分出来,然后对他进行转换,最后比较大小返回到原数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #define ll long long
class Solution {
public:
vector<int> sortJumbled(vector<int>& mapping, vector<int>& nums) {
sort(nums.begin(),nums.end(),[&](int a,int b){
ll va=0,vb=0,base=1;
if(a==0) va=mapping[0];
else {
base=1;
while(a){
int x=a%10;a/=10;
va=va+base*mapping[x];
base*=10;
}
}
if(b==0) vb=mapping[0];else{
base=1;
while(b){
int x=b%10;b/=10;
vb=vb+base*mapping[x];
base*=10;
}
}
return va<vb;
});
return nums;
}
};
|
2192.有向无环图中一个节点的所有祖先
给你一个正整数 n ,它表示一个 有向无环图 中节点的数目,节点编号为 0 到 n - 1 (包括两者)。
给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。
请你返回一个数组 answer,其中 answer[i]是第 i 个节点的所有 祖先 ,这些祖先节点 升序 排序。
如果 u 通过一系列边,能够到达 v ,那么我们称节点 u 是节点 v 的 祖先 节点。
示例 1:
1
2
3
4
5
6
7
8
9
10
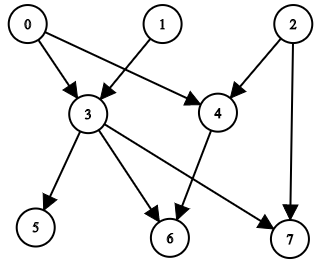
| 输入:n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出:[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释:
上图为输入所对应的图。
- 节点 0 ,1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ,1 和 3 。
- 节点 6 有 5 个祖先 0 ,1 ,2 ,3 和 4 。
- 节点 7 有 4 个祖先 0 ,1 ,2 和 3 。
|
示例 2:
1
2
3
4
5
6
7
8
9
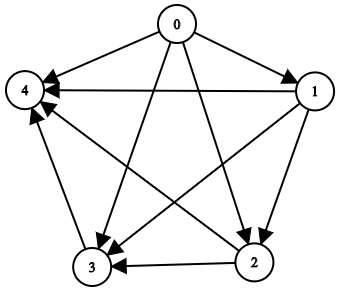
| 输入:n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
输出:[[],[0],[0,1],[0,1,2],[0,1,2,3]]
解释:
上图为输入所对应的图。
- 节点 0 没有任何祖先。
- 节点 1 有 1 个祖先 0 。
- 节点 2 有 2 个祖先 0 和 1 。
- 节点 3 有 3 个祖先 0 ,1 和 2 。
- 节点 4 有 4 个祖先 0 ,1 ,2 和 3 。
|
提示:
1 <= n <= 10000 <= edges.length <= min(2000, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi <= n - 1fromi != toi- 图中不会有重边。
- 图是 有向 且 无环 的。
分析:
根据题目意思
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| const int MAXN=1e3+10;
vector<int> ans[MAXN];
bool dirs[MAXN][MAXN];
queue<int> que;
class Solution {
public:
void bfs(int s){
while(!que.empty()) que.pop();
que.push(s);
dirs[s][s]=true;
while(!que.empty()){
int x=que.front();
que.pop();
for(int v:ans[x]){
if(!dirs[s][v]){
dirs[s][v]=true;
que.push(v);
}
}
}
}
vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
for(int i=0;i<=n;i++){
ans[i].clear();
for(int j=0;j<=n;j++) dirs[i][j]=false;
}
for(vector<int>& e:edges) ans[e[0]].push_back(e[1]);
for(int i=0;i<n;i++)bfs(i);
vector<vector<int>> res;
for(int i=0;i<n;i++){
vector<int> cur;
for(int j=0;j<n;j++){
if(j!=i&&dirs[j][i]) cur.push_back(j);
}
res.push_back(cur);
}
return res;
}
};
|
2193.得到回文串的最少操作次数
给你一个只包含小写英文字母的字符串 s 。
每一次 操作 ,你可以选择 s 中两个 相邻 的字符,并将它们交换。
请你返回将 s 变成回文串的 最少操作次数 。
注意 ,输入数据会确保 s 一定能变成一个回文串。
示例 1:
1
2
3
4
5
6
7
| 输入:s = "aabb"
输出:2
解释:
我们可以将 s 变成 2 个回文串,"abba" 和 "baab" 。
- 我们可以通过 2 次操作得到 "abba" :"aabb" -> "abab" -> "abba" 。
- 我们可以通过 2 次操作得到 "baab" :"aabb" -> "abab" -> "baab" 。
因此,得到回文串的最少总操作次数为 2 。
|
示例 2:
1
2
3
4
5
6
7
| 输入:s = "letelt"
输出:2
解释:
通过 2 次操作从 s 能得到回文串 "lettel" 。
其中一种方法是:"letelt" -> "letetl" -> "lettel" 。
其他回文串比方说 "tleelt" 也可以通过 2 次操作得到。
可以证明少于 2 次操作,无法得到回文串。
|
提示:
1 <= s.length <= 2000s 只包含小写英文字母。s 可以通过有限次操作得到一个回文串。
分析:
考虑左指针与右指针,由于数据范围过小,因此考虑贪心
情况:
原题链接
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
int minMovesToMakePalindrome(string s) {
int n=s.size();
int ans=0;
for(int i=0;i<n/2;i++){
int left=i;
int right=n-left-1;
while(s[right]!=s[left]){
right--;
}
if (left == right) {
swap(s[left], s[left + 1]);
ans++;
i--;
} else {
for (int j = right; j < n - left - 1; j++) {
swap(s[j], s[j + 1]);
ans++;
}
}
}
return ans;
}
};
|

