第283场周赛解答

第283场周赛

链接↓

第283场周赛

2194.Excel 表中某个范围内的单元格

Excel 表中的一个单元格 (r, c) 会以字符串的形式进行表示，其中：

col> 即单元格的列号 c 。用英文字母表中的字母标识。

- 例如，第 1 列用 'A' 表示，第 2 列用 'B' 表示，第 3 列用 'C' 表示，以此类推。

即单元格的行号 r 。第 r 行就用整数 r 标识。

给你一个格式为 ":" 的字符串 s ，其中表示 `c1` 列，表示 r1 行，表示 `c2` 列，表示 r2 行，并满足 r1 <= r2 且 c1 <= c2 。

找出所有满足 r1 <= x <= r2 且 c1 <= y <= c2 的单元格，并以列表形式返回。单元格应该按前面描述的格式用 字符串 表示，并以 非递减 顺序排列（先按列排，再按行排）。

示例 1：

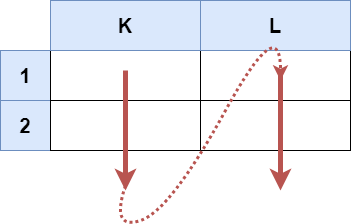
输入：s = "K1:L2"
输出：["K1","K2","L1","L2"]
解释：
上图显示了列表中应该出现的单元格。
红色箭头指示单元格的出现顺序。

示例 2：

输入：s = "A1:F1"
输出：["A1","B1","C1","D1","E1","F1"]
解释：
上图显示了列表中应该出现的单元格。 
红色箭头指示单元格的出现顺序。

提示：

s.length == 5
'A' <= s[0] <= s[3] <= 'Z'
'1' <= s[1] <= s[4] <= '9'
s 由大写英文字母、数字、和 ':' 组成

分析

模拟

class Solution {
public:
    vector<string> cellsInRange(string s) {
     vector<string> ans;
     int r1=s[0],r2=s[1],l1=s[3],l2=s[4];
     for(int i=r1;i<=l1;i++) {
         for(int j=r2;j<=l2;j++){
            string s="";
            s+=char(i);
            s+=char(j);
            ans.push_back(s);
         }
     }  
     return ans;
    }
};

2195.向数组中追加 K 个整数

给你一个整数数组 nums 和一个整数 k 。请你向 nums 中追加 k 个未出现在 nums 中的、互不相同 的正整数，并使结果数组的元素和最小。

返回追加到 nums 中的 k 个整数之和。

示例 1：

输入：nums = [1,4,25,10,25], k = 2
输出：5
解释：在该解法中，向数组中追加的两个互不相同且未出现的正整数是 2 和 3 。
nums 最终元素和为 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70 ，这是所有情况中的最小值。
所以追加到数组中的两个整数之和是 2 + 3 = 5 ，所以返回 5 。

示例 2：

输入：nums = [5,6], k = 6
输出：25
解释：在该解法中，向数组中追加的两个互不相同且未出现的正整数是 1 、2 、3 、4 、7 和 8 。
nums 最终元素和为 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36 ，这是所有情况中的最小值。
所以追加到数组中的两个整数之和是 1 + 2 + 3 + 4 + 7 + 8 = 25 ，所以返回 25 。

提示：

1 <= nums.length <= 105
1 <= nums[i], k <= 109

分析

模拟，根据等差公式求和，最后对1~k范围内，若原数组中已含有该元素，将其替换。

class Solution {
#define ll long long
unordered_map<int,bool> vis;
    set<int> cur_v;
public:
    long long minimalKSum(vector<int>& nums, int k) {
        ll ans=1ll*(1+k)*k/2ll;
        
        int cur=k+1;
        vis.clear();cur_v.clear();
        for(int v:nums){
            vis[v]=true;
            cur_v.insert(v);
        }
        for(int v:cur_v){
            if(v<=k){
                while(vis[cur]) cur+=1;
                ans+=cur-v;
                vis[cur]=true;
            }
        }
        return ans;
    }
};

2196.根据描述创建二叉树

给你一个二维整数数组 descriptions ，其中 descriptions[i] = [parenti, childi, isLefti] 表示 parenti 是 childi 在 二叉树 中的 父节点，二叉树中各节点的值 互不相同 。此外：

如果 isLefti == 1 ，那么 childi 就是 parenti 的左子节点。
如果 isLefti == 0 ，那么 childi 就是 parenti 的右子节点。

请你根据 descriptions 的描述来构造二叉树并返回其 根节点 。

测试用例会保证可以构造出有效的二叉树。

示例 1：

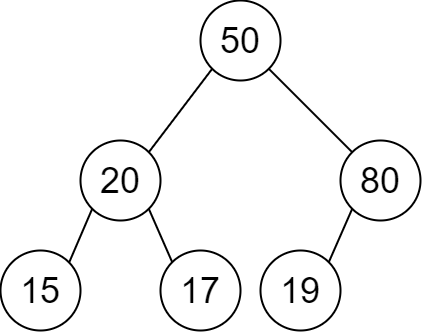
输入：descriptions = [[20,15,1],[20,17,0],[50,20,1],[50,80,0],[80,19,1]]
输出：[50,20,80,15,17,19]
解释：根节点是值为 50 的节点，因为它没有父节点。
结果二叉树如上图所示。

示例 2：

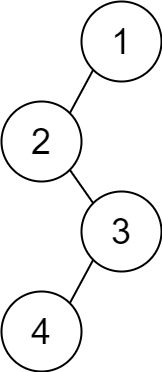
输入：descriptions = [[1,2,1],[2,3,0],[3,4,1]]
输出：[1,2,null,null,3,4]
解释：根节点是值为 1 的节点，因为它没有父节点。 
结果二叉树如上图所示。

提示：

1 <= descriptions.length <= 104
descriptions[i].length == 3
1 <= parenti, childi <= 105
0 <= isLefti <= 1
descriptions 所描述的二叉树是一棵有效二叉树

分析

模拟

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
unordered_map<int,TreeNode*> root;
set<int> indeg;
set<int> apps;
public:
    TreeNode* getNode(int x){
        if(apps.count(x)==0){
            apps.insert(x);
            TreeNode *rt=new TreeNode(x);
            root[x]=rt;
        }
        return root[x];
        }
    TreeNode* createBinaryTree(vector<vector<int>>& descriptions) {
        root.clear();
        indeg.clear();
        apps.clear();
        for(vector<int>& des:descriptions){
            int fa=des[0],ch=des[1],lf=des[2];
            TreeNode *f=getNode(fa);
            TreeNode *c=getNode(ch);
            indeg.insert(ch);
            if(lf==1) f->left=c;
            else f->right=c;
        }
        for(int x:apps){
            if(indeg.count(x)==0) return root[x];
        }
        return NULL;
    }
};

2197.替换数组中的非互质数

给你一个整数数组 nums 。请你对数组执行下述操作：

从 nums 中找出任意两个相邻的 非互质 数。
如果不存在这样的数，终止这一过程。
否则，删除这两个数，并替换为它们的 最小公倍数（Least Common Multiple，LCM）。
只要还能找出两个相邻的非互质数就继续重复这一过程。

返回修改后得到的最终数组。可以证明的是，以任意顺序替换相邻的非互质数都可以得到相同的结果。

生成的测试用例可以保证最终数组中的值 小于或者等于 108 。

两个数字 x 和 y 满足 非互质数 的条件是：GCD(x, y) > 1 ，其中 GCD(x, y) 是 x 和 y 的 最大公约数 。

示例 1 ：

输入：nums = [6,4,3,2,7,6,2]
输出：[12,7,6]
解释：
- (6, 4) 是一组非互质数，且 LCM(6, 4) = 12 。得到 nums = [12,3,2,7,6,2] 。
- (12, 3) 是一组非互质数，且 LCM(12, 3) = 12 。得到 nums = [12,2,7,6,2] 。
- (12, 2) 是一组非互质数，且 LCM(12, 2) = 12 。得到 nums = [12,7,6,2] 。
- (6, 2) 是一组非互质数，且 LCM(6, 2) = 6 。得到 nums = [12,7,6] 。
现在，nums 中不存在相邻的非互质数。
因此，修改后得到的最终数组是 [12,7,6] 。
注意，存在其他方法可以获得相同的最终数组。

示例 2 ：

输入：nums = [2,2,1,1,3,3,3]
输出：[2,1,1,3]
解释：
- (3, 3) 是一组非互质数，且 LCM(3, 3) = 3 。得到 nums = [2,2,1,1,3,3] 。
- (3, 3) 是一组非互质数，且 LCM(3, 3) = 3 。得到 nums = [2,2,1,1,3] 。
- (2, 2) 是一组非互质数，且 LCM(2, 2) = 2 。得到 nums = [2,1,1,3] 。
现在，nums 中不存在相邻的非互质数。 
因此，修改后得到的最终数组是 [2,1,1,3] 。 
注意，存在其他方法可以获得相同的最终数组。

提示：

1 <= nums.length <= 105
1 <= nums[i] <= 105
生成的测试用例可以保证最终数组中的值 小于或者等于 108 。

分析：

栈模拟

class Solution {
public:
    vector<int> replaceNonCoprimes(vector<int>& nums) {
        vector<int> ans;
        for (int num : nums) {
            ans.push_back(num);
            int n = ans.size();
            while (n >= 2 && gcd(ans[n - 2], ans[n - 1]) > 1) {
                int r = ans.back();
                ans.pop_back();
                ans.back() *= r / gcd(ans.back(), r);
                n--;
            }
        }
        return ans;
    }
};