玖的数学&算法录
0%

第71场双周赛解答

发表于 更新于
本文字数： 6.3k 阅读时长 ≈ 6 分钟

第71场双周赛

链接↓

第71场双周赛

5984.拆分数位后四位数字的最小和

给你一个四位 正 整数 num 。请你使用 num 中的 数位 ，将 num 拆成两个新的整数 new1 和 new2 。new1 和 new2 中可以有 前导 0 ，且 num 中 所有 数位都必须使用。

  • 比方说，给你 num = 2932 ，你拥有的数位包括：两个 2 ，一个 9 和一个 3 。一些可能的 [new1, new2] 数对为 [22, 93]，[23, 92]，[223, 9] 和 [2, 329] 。

请你返回可以得到的 new1 和 new2 的 最小 和。

示例 1：

1
2
3
4
输入：num = 2932
输出：52
解释：可行的 [new1, new2] 数对为 [29, 23] ，[223, 9] 等等。
最小和为数对 [29, 23] 的和：29 + 23 = 52 。

示例 2：

1
2
3
4
输入：num = 4009
输出：13
解释：可行的 [new1, new2] 数对为 [0, 49] ，[490, 0] 等等。
最小和为数对 [4, 9] 的和：4 + 9 = 13 。

提示：

  • 1000 <= num <= 9999

分析：

对于本题我们易知 new1 和 new2 必然是个（前导为0，例：01，02…，09）/十位数，因此我们直接对 num 进行拆解出个、十、百、千即可

设立一个容器，储存四个独立的数字，进行一次排序，即

$$a\leq b\leq c\leq d$$

自然结果就是

$$\displaystyle ans=10*(a+b)+c+d$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int minimumSum(int num) {
    int ans=0;
    int a=num/1000;
    int b=num/100%10;
    int c=num/10%10;
    int d=num%10;
    vector<int> res;
    res.push_back(a);
        res.push_back(b);
        res.push_back(c);
        res.push_back(d);
    sort(res.begin(),res.end());
    ans=res[0]*10+res[1]*10+res[2]+res[3];
    return ans;
    }
};

5985. 根据给定数字划分数组

给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列，使得以下条件均成立：

  • 所有小于 pivot 的元素都出现在所有大于 pivot 的元素 之前 。
  • 所有等于 pivot 的元素都出现在小于和大于 pivot 的元素 中间 。
  • 小于 pivot 的元素之间和大于 pivot 的元素之间的 相对顺序 不发生改变。
  • 更正式的，考虑每一对 pi，pj ，pi 是初始时位置 i 元素的新位置，pj 是初始时位置 j 元素的新位置。对于小于 pivot 的元素，如果 i < j 且 nums[i] < pivot 和 nums[j] < pivot 都成立，那么 pi < pj 也成立。类似的，对于大于 pivot 的元素，如果 i < j 且 nums[i] > pivot 和 nums[j] > pivot 都成立，那么 pi < pj 。

请你返回重新排列 nums 数组后的结果数组。

示例 1：

1
2
3
4
5
6
输入：nums = [9,12,5,10,14,3,10], pivot = 10
输出：[9,5,3,10,10,12,14]
解释：
元素 9 ，5 和 3 小于 pivot ，所以它们在数组的最左边。
元素 12 和 14 大于 pivot ，所以它们在数组的最右边。
小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [9, 5, 3] 和 [12, 14] ，它们在结果数组中的相对顺序需要保留。

示例 2：

1
2
3
4
5
6
输入：nums = [-3,4,3,2], pivot = 2
输出：[-3,2,4,3]
解释：
元素 -3 小于 pivot ，所以在数组的最左边。
元素 4 和 3 大于 pivot ，所以它们在数组的最右边。
小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [-3] 和 [4, 3] ，它们在结果数组中的相对顺序需要保留。

提示：

  • 1 <= nums.length <= 105
  • -106 <= nums[i] <= 106
  • pivot 等于 nums 中的一个元素。

分析:

本题与第277场周赛的第二题2149. 按符号重排数组 思路十分相似

实际上该题的意思即“荷兰国旗问题”

见算法笔记（01）：排序中的算法 中的6.快速排序的引出题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<int> pivotArray(vector<int>& nums, int pivot) {
    vector<int> less,more,equal;
    for(int i=0;i<nums.size();i++){
        if(nums[i]<pivot){
            less.push_back(nums[i]);
        }
        else if(nums[i]==pivot){
            equal.push_back(nums[i]);
        }
        else{
            more.push_back(nums[i]);
        }
    }
        vector<int> ans;
        for(int i=0;i<less.size();i++){
            ans.push_back(less[i]);
        }
        for(int i=0;i<equal.size();i++){
            ans.push_back(equal[i]);
        }
        for(int i=0;i<more.size();i++){
            ans.push_back(more[i]);
        }
        return ans;
    }
};

这题更是__题，建议更换难度。

5986. 设置时间的最少代价

常见的微波炉可以设置加热时间，且加热时间满足以下条件：

  • 至少为 1 秒钟。
  • 至多为 99 分 99 秒。

你可以 最多 输入 4 个数字 来设置加热时间。如果你输入的位数不足 4 位，微波炉会自动加 前缀 0 来补足 4 位。微波炉会将设置好的四位数中，前 两位当作分钟数，后 两位当作秒数。它们所表示的总时间就是加热时间。比方说：

  • 你输入 9 5 4 （三个数字），被自动补足为 0954 ，并表示 9 分 54 秒。
  • 你输入 0 0 0 8 （四个数字），表示 0 分 8 秒。
  • 你输入 8 0 9 0 ，表示 80 分 90 秒。
  • 你输入 8 1 3 0 ，表示 81 分 30 秒。

给你整数 startAt ，moveCost ，pushCost 和 targetSeconds 。一开始，你的手指在数字 startAt 处。将手指移到 任何其他数字 ，需要花费 moveCost 的单位代价。每 输入你手指所在位置的数字一次，需要花费 pushCost 的单位代价。

要设置 targetSeconds 秒的加热时间，可能会有多种设置方法。你想要知道这些方法中，总代价最小为多少。

请你能返回设置 targetSeconds 秒钟加热时间需要花费的最少代价。

请记住，虽然微波炉的秒数最多可以设置到 99 秒，但一分钟等于 60 秒。

示例 1：

img

1
2
3
4
5
6
7
8
9
10
11
12
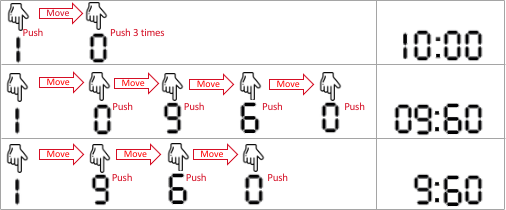
输入：startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
输出：6
解释：以下为设置加热时间的所有方法。
- 1 0 0 0 ，表示 10 分 0 秒。
  手指一开始就在数字 1 处，输入 1 （代价为 1），移到 0 处（代价为 2），输入 0（代价为 1），输入 0（代价为 1），输入 0（代价为 1）。
  总代价为：1 + 2 + 1 + 1 + 1 = 6 。这是所有方案中的最小代价。
- 0 9 6 0，表示 9 分 60 秒。它也表示 600 秒。
  手指移到 0 处（代价为 2），输入 0 （代价为 1），移到 9 处（代价为 2），输入 9（代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。
  总代价为：2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12 。
- 9 6 0，微波炉自动补全为 0960 ，表示 9 分 60 秒。
  手指移到 9 处（代价为 2），输入 9 （代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。
  总代价为：2 + 1 + 2 + 1 + 2 + 1 = 9 。

示例 2：

img

1
2
3
4
5
输入：startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
输出：6
解释：最优方案为输入两个数字 7 6，表示 76 秒。
手指移到 7 处（代价为 1），输入 7 （代价为 2），移到 6 处（代价为 1），输入 6（代价为 2）。总代价为：1 + 2 + 1 + 2 = 6
其他可行方案为 0076 ，076 ，0116 和 116 ，但是它们的代价都比 6 大。

提示：

  • 0 <= startAt <= 9
  • 1 <= moveCost, pushCost <= 105
  • 1 <= targetSeconds <= 6039

分析：

首先对于本题，我们需要将时间转化成几分几秒，特别地（虽然微波炉的秒数最多可以设置到 99 秒，但一分钟等于 60 秒）

1.求出分钟（i），秒（j）

2.下步骤同题目1分析

3.先跳过所有数字0（能省去移动一次的代价），后判断当前所需数字与所在数组是否相同，相同输入，不相同输出，求出对应时间res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int minCostSetTime(int s, int m, int p, int ts) {
    int ans=1<<30,c[4];
    for(int i=0;i<=99;i++){
        int j=ts-i*60;
        if(j<0||j>99){
            continue;
        }
        c[0]=i/10,c[1]=i%10;
        c[2]=j/10,c[3]=j%10;
        int d=s,res=0;
        bool flag=0;
        for(int j=0;j<4;j++){
            if(c[j]){
                flag=1;
            }
            if(flag){
                if(c[j]!=d)
                    res+=m,d=c[j];
                res+=p;
            }
        }
        ans=min(ans,res);
    }
    return ans;
    }
};

5987. 删除元素后和的最小差值

给你一个下标从 0 开始的整数数组 nums ，它包含 3 * n 个元素。

你可以从 nums 中删除 恰好 n 个元素，剩下的 2 * n 个元素将会被分成两个 相同大小 的部分。

  • 前面 n 个元素属于第一部分，它们的和记为 sumfirst 。
  • 后面 n 个元素属于第二部分，它们的和记为 sumsecond 。

两部分和的 差值 记为 sumfirst - sumsecond 。

  • 比方说，sumfirst = 3 且 sumsecond = 2 ，它们的差值为 1 。
  • 再比方，sumfirst = 2 且 sumsecond = 3 ，它们的差值为 -1 。

请你返回删除 n 个元素之后，剩下两部分和的 差值的最小值 是多少。

示例 1：

1
2
3
4
5
6
7
8
输入：nums = [3,1,2]
输出：-1
解释：nums 有 3 个元素，所以 n = 1 。
所以我们需要从 nums 中删除 1 个元素，并将剩下的元素分成两部分。
- 如果我们删除 nums[0] = 3 ，数组变为 [1,2] 。两部分和的差值为 1 - 2 = -1 。
- 如果我们删除 nums[1] = 1 ，数组变为 [3,2] 。两部分和的差值为 3 - 2 = 1 。
- 如果我们删除 nums[2] = 2 ，数组变为 [3,1] 。两部分和的差值为 3 - 1 = 2 。
两部分和的最小差值为 min(-1,1,2) = -1 。

示例 2：

1
2
3
4
5
6
输入：nums = [7,9,5,8,1,3]
输出：1
解释：n = 2 。所以我们需要删除 2 个元素，并将剩下元素分为 2 部分。
如果我们删除元素 nums[2] = 5 和 nums[3] = 8 ，剩下元素为 [7,9,1,3] 。和的差值为 (7+9) - (1+3) = 12 。
为了得到最小差值，我们应该删除 nums[1] = 9 和 nums[4] = 1 ，剩下的元素为 [7,5,8,3] 。和的差值为 (7+5) - (8+3) = 1 。
观察可知，最优答案为 1 。

提示：

  • nums.length == 3 * n
  • 1 <= n <= 105
  • 1 <= nums[i] <= 105

分析：①

不妨约定

$$\displaystyle sum_{first}=A,sum_{Delete}=B,sum_{Second}=Sum-A-B$$

易知

$$Different=A-(Sum-A-B)=2A+B-Sum$$ –①

根据题意,若想Different最小，只需要A与B最小即可。

将数组中间分一半,得

$$num_{left}=n+a,num_{right}=n+b$$

其中a+b=n

同时根据①可知 A的权重＞B的权重

因此取数组左边最小的n个数,贡献给A，取数组右边最大的n个数，贡献给B

下面考虑使用优先队列处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
const int MAXN=1e5+50;
priority_queue<long long> que;

long long suff[MAXN]; //suff[i]=后n+i个数字中,最小的i个数字之和是多少
long long pref[MAXN]; //pref[i]=前n+i个数字中,最大的i个数字之和是多少
long long ssum[MAXN*3];

class Solution {
public:
    long long minimumDifference(vector<int>& nums) {
     int n=nums.size();n/=3;
    ssum[0]=0;
    for(int i=1;i<=n+n+n;i++) ssum[i]=ssum[i-1]+nums[i-1];
        
    while(!que.empty()) que.pop();
        for(int i=n+n;i<n+n+n;i++) que.push(-nums[i]);
        suff[0]=0;
        for(int i=1;i<=n;i++){
            que.push(-nums[n+n-i]);
            suff[i]=suff[i-1]-que.top();
            que.pop();
        }
     while(!que.empty()) que.pop();
        pref[0]=0;
        for(int i=0;i<n;i++) que.push(nums[i]);
        for(int i=1;i<=n;i++){
            que.push(nums[n-1+i]);
            pref[i]=pref[i-1]+que.top();
            que.pop();
        }
        
        long long ans=ssum[n]-(ssum[n+n+n]-ssum[n+n]);
        for(int i=0;i<=n;i++){
            long long B=suff[n-i]+pref[i];
            long long A=ssum[n+i]-pref[i];
            long long cur=2*A+B-ssum[n+n+n];
            ans=min(ans,cur);
        }
        return ans;
    }
};

参考：【算法实况】新年好呀，年后第一场双周赛~ - 力扣双周赛 - LeetCode Biweekly 71